Сумма углов выпуклого многоугольника - это важная геометрическая характеристика, которая зависит от количества сторон фигуры. Данное свойство широко используется в геометрии для решения различных задач и доказательства теорем.
Содержание
Сумма углов выпуклого многоугольника - это важная геометрическая характеристика, которая зависит от количества сторон фигуры. Данное свойство широко используется в геометрии для решения различных задач и доказательства теорем.
Основная теорема о сумме углов
Сумма внутренних углов выпуклого n-угольника вычисляется по формуле: S = (n - 2) × 180°, где n - количество сторон многоугольника.
Доказательство теоремы
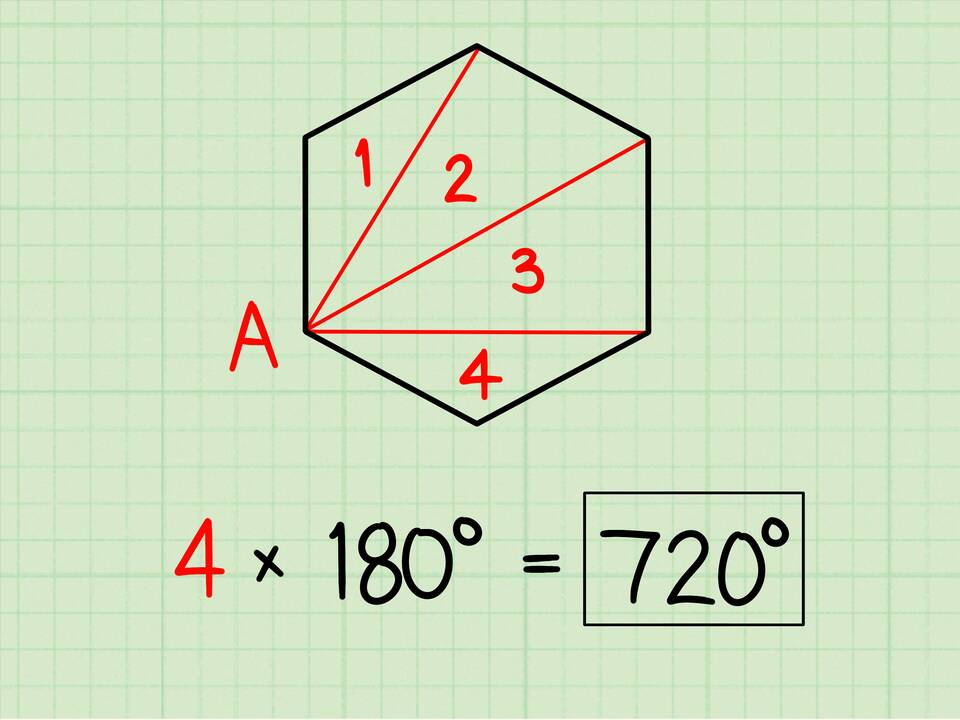
Теорема доказывается методом разбиения многоугольника на треугольники:
- Выбираем произвольную вершину многоугольника
- Проводим диагонали из этой вершины ко всем несмежным вершинам
- Многоугольник разбивается на (n - 2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов многоугольника равна сумме углов всех полученных треугольников
Примеры для различных многоугольников
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
| Шестиугольник | 6 | (6-2)×180° = 720° |
Сумма внешних углов выпуклого многоугольника
Для любого выпуклого n-угольника сумма внешних углов, взятых по одному при каждой вершине, равна 360° независимо от количества сторон.
Свойства внешних углов:
- Внешний угол дополняет внутренний до 180°
- Сумма внутреннего и внешнего угла при каждой вершине равна 180°
- Для вычисления одного внешнего угла правильного n-угольника: 360°/n
Применение в задачах
Знание суммы углов многоугольника позволяет:
- Находить неизвестные углы многоугольников
- Доказывать свойства геометрических фигур
- Решать задачи на построение
- Определять возможность существования многоугольников с заданными параметрами
Пример решения задачи
В пятиугольнике четыре угла равны 110°, 80°, 95° и 125°. Найдите пятый угол.
- Сумма углов пятиугольника: (5-2)×180° = 540°
- Сумма известных углов: 110° + 80° + 95° + 125° = 410°
- Неизвестный угол: 540° - 410° = 130°
Особенности выпуклых многоугольников
Важно отметить, что приведенные формулы работают именно для выпуклых многоугольников, которые обладают следующими свойствами:
- Все внутренние углы меньше 180°
- Любая прямая, содержащая сторону многоугольника, не пересекает другие стороны
- Все диагонали лежат внутри многоугольника
Для невыпуклых (вогнутых) многоугольников сумма углов также вычисляется по формуле (n-2)×180°, но методы доказательства могут отличаться.
