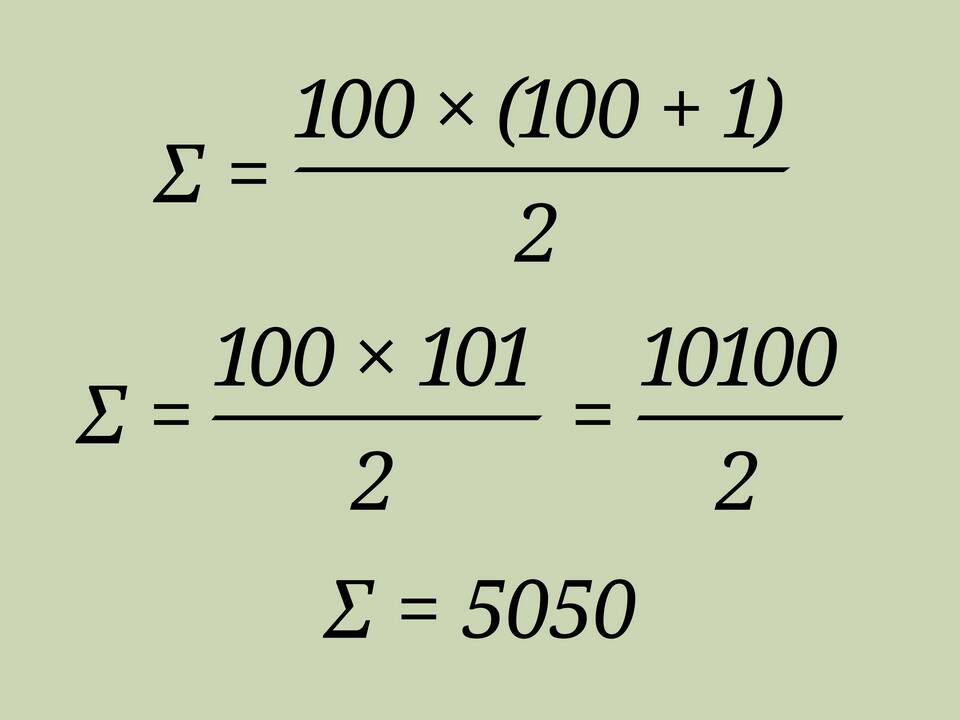В математике часто возникает вопрос о соотношении суммы чисел и их отдельных слагаемых. Разберемся, в каких случаях сумма может быть больше своих слагаемых, а в каких - меньше.
Содержание
В математике часто возникает вопрос о соотношении суммы чисел и их отдельных слагаемых. Разберемся, в каких случаях сумма может быть больше своих слагаемых, а в каких - меньше.
Основные математические принципы
Сумма чисел всегда подчиняется определенным закономерностям:
- Для положительных чисел сумма всегда больше каждого отдельного слагаемого
- Для отрицательных чисел сумма может быть меньше каждого слагаемого
- При смешанных знаках результат зависит от соотношения чисел
Примеры сравнения
| Числа | Сумма | Сравнение |
| 5, 7, 3 | 15 | Сумма больше каждого слагаемого |
| -2, -4, -1 | -7 | Сумма меньше каждого слагаемого |
| 6, -3, 2 | 5 | Сумма больше отрицательных, но меньше положительных слагаемых |
Математические свойства сумм
Рассмотрим важные свойства сумм чисел:
- Коммутативность: порядок слагаемых не влияет на сумму
- Ассоциативность: группировка слагаемых не меняет результат
- Монотонность: увеличение слагаемых увеличивает сумму
Особые случаи
- Сумма числа с нулем равна самому числу
- Сумма противоположных чисел дает ноль
- Бесконечные ряды могут иметь конечную сумму
Практическое применение
Понимание соотношения суммы и слагаемых важно в:
- Финансовых расчетах
- Статистическом анализе
- Физических измерениях
- Программировании и алгоритмах
